Free Online 11+ Maths Tutoring – Open to All
Free Online 11+ Maths Tutoring – Open to All Hi! I’m Rithvik Muthuvelu , a GCSE student at King Edward’s School, Birmingham , and I’m offering free weekly online maths sessions to help students prepare for the 11+ entrance exams . These sessions are open to anyone who wants to improve their maths skills—no school restrictions. What You’ll Get Free weekly online maths classes Focused 11+ preparation : problem-solving, arithmetic, word problems, exam strategies Small-group format for better interaction Ideal for Year 4 and Year 5 students How to Join Weekly Session: Saturdays at 2:00 PM Google Meet Link: https://meet.google.com/nrk-iwmh-gij Contact Email: rithvikmu1@gmail.com If your child is preparing for the 11+ and would like extra support, feel free to join the class or get in touch. Looking forward to helping more students learn and grow! — Rithvik Muthuvelu
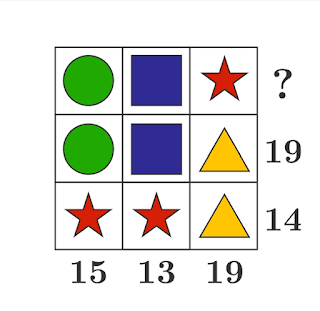
The star = r
ReplyDeleteThe circle = g
The square = b
The triangle = y
So if we just look at r and y the we'll see that:
2r + y = 14
r + 2y = 19
____________
and if you add these two equations together you will get => 3r + 3y = 33
if 3r + 3y = 33 then r + y = 11 and 2r + y = 14 then r = 3.
Also if 2r + y = 14 and r = 3 then it would be 2 * 3 + y = 14 so 6 + y = 14 and y = 8.
Now lets look at g and r:
So we know that 2g + r = 15 and r = 3 so we can substitute that in:
2g + 3 = 15
2g = 15 - 3
2g = 12
g = 6
Now let us look at the equation g + b + y = 19:
We already know that g = 6 and y = 8, so we can substitute that in:
6 + b + 8 = 19
14 + b = 19
b = 19 - 14
b = 5
Finally, lets look at the question mark equation:
g + b + r = ?
We already know g, b and r so we can substitute those in:
6 + 5 + 3 = ?
? = 14
so we get our answer
? = 14
well done riti
Delete